The Logic Calculator is a free app on the iOS (iPhones and iPads), Android (phones, tablets, etc.) and Windows (desktops, laptops, tablets, xbox ones) platforms. I coded it to allow users of propositional logic to perform operations with the same ease as that offered by a mathematical calculator. Its design is such that it hopefully facilitates learners of logic by providing feedback on what makes input well-formed. For more details on this and, more generally, on how to operate the calculator, please consult the information section below. As of this version, the calculator is restricted to semantic operations.
To report bugs or to request the addition of new functions in future versions of this app please send your e-mail to: logic(/a-t\)votsis.org
Copyright: (c) 2019 Ioannis Votsis
Privacy Policy: In a nutshell, the app is free and collects no information. For more details read the Privacy Policy PDF.



Information:
(A) INPUT ALLOWED:
Just like a mathematical calculator, the logic calculator allows its users to compute results from various inputs. The inputs in this case are the logical formulae of propositional logic. For simplicity, we can call these formulae 'sentences'. The calculator offers a wide range of input. One can use up to six different letter variables ('P', 'Q', 'R', 'S', 'T', 'U') to denote atomic sentences. Moreover, the calculator allows the user to give as input compound (also known as 'complex' or 'molecular') sentences. These are sentences that employ one or more of the five logical connectives ('¬', '&', '∨', '→', '↔'), e.g. sentences '¬P', 'P&Q' and '(P∨Q)↔R'. Additionally, the calculator allows input in the form of sets of sentences. The sets are denoted by curly brackets, e.g. '{P, P→Q}', '{P, ¬P}', '{Q, R→¬Q, R∨¬Q}'. Finally, the calculator allows as input arguments where the symbol '╞' signifies the entailment relation. If there are two or more sentences that make up the premises of an argument, they must be listed as a set followed by the entailment relation symbol and, finally, the sentence purporting to be the conclusion. Here are three examples: '{P}╞P', '{P, P→Q}╞Q', '{P, P→Q, Q→R, R→S}╞S'.
(B) OUTPUT PRODUCED:
Three types of output are produced:
(1) The calculator determines whether the input is well-formed. In other words, it determines whether the input is syntactically correct and lets the user know. When the input is not well-formed, errors are indicated. More on this below.
(2) In case the input is indeed well-formed, the calculator proceeds to determine its properties. For individual sentences (atomic or compound), it determines whether they are tautologies, contradictions or contingent. For sets, it determines whether they are consistent or inconsistent. For arguments, it determines whether they are valid or invalid.
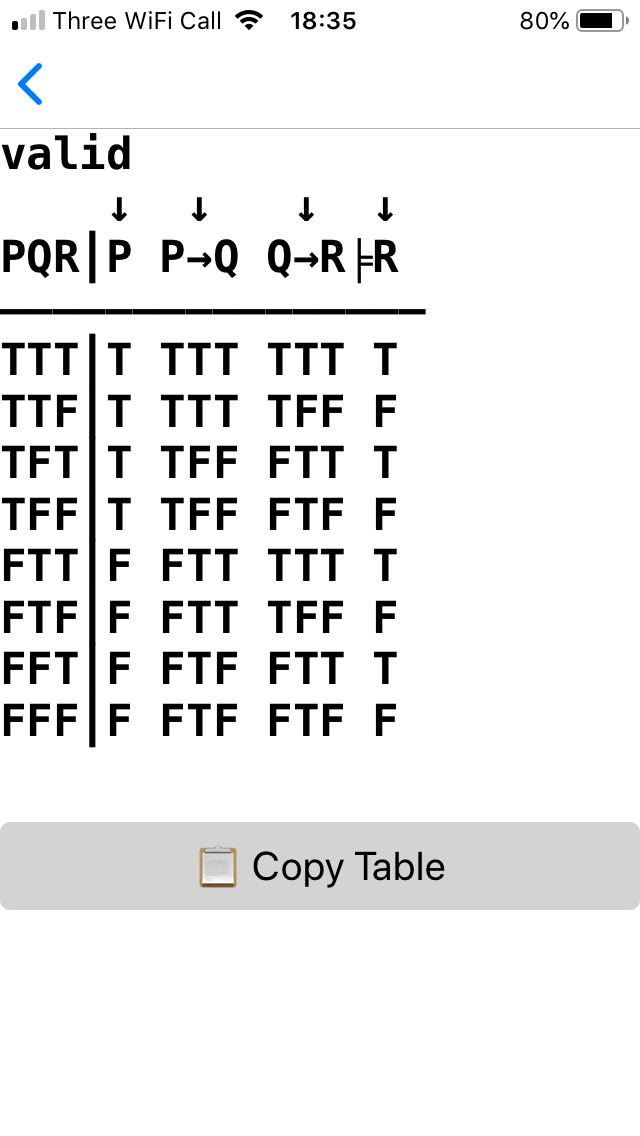
(3) Provided the input is well-formed, the calculator is also able to produce truth tables which the user can copy and paste into other apps and documents.
(C) INSTRUCTIONS:
Only two buttons produce output: 'ENTER' and 'TABLE'. Here's how to use them. First, we need some input. Suppose that input is 'P&Q'. To insert this input is as easy as it sounds. Press button 'P', then press button '&' and finally press button 'Q'. To determine whether the input is well-formed, you can then press either the 'ENTER' button or the 'TABLE' button. If you press the 'ENTER' button, the calculator will remain on the same page and will just indicate the output just below the input and above the calculator buttons. As input 'P&Q' is indeed well-formed, the calculator will produce the output 'contingent sentence' as the input sentence is neither a tautology nor a contradiction. If you press the 'TABLE' button instead, you will also be shown that sentence's truth table on another page in addition to being told that it is a contingent sentence. The truth-table also indicates, through the use of the downward arrow '↓', where the main connective is located in each sentence. In the case at hand, the main connective is the ampersand symbol '&'. In cases of atomic sentences, where there is no main connective, the downward arrow appears over each atomic sentence. Whenever a truth table is produced, the user has the choice of returning to the calculator or copying the truth table. Take another input that is not a well-formed sentence, e.g. 'P&&Q'. The app will indicate this on the main calculator page just below the input with the phrase 'not well-formed'. This is regardless of whether the user pressed 'ENTER' or 'TABLE' as no truth table is produced when the input is not well-formed. Also indicated in cases where the input is not well-formed is/are the location(s) of error(s) through the use of red underlining. In the case at hand, the second '&' is underlined in red. More information about errors can be found below. To determine whether a set is consistent or inconsistent, the user must provide as input a set. Suppose the set is {P, ¬P}. To open a set press the '{...}' button. Then insert the two sentences and separate them by a comma using the comma ',' button. To close a set, press the '{...}' button a second time. Once more, the user can either press the 'ENTER' or 'TABLE' buttons. The first button yields the output that, in this case, the set is inconsistent. The second outputs the corresponding truth table in addition to the judgement that, in this case, the set is inconsistent. To determine whether an argument is valid or invalid, one needs to provide an argument as input. Suppose that argument is {P∨Q, ¬Q}╞P. As before, the user can either press 'ENTER' or 'TABLE' to produce output. The first button yields the output that the argument in this case is valid. The second outputs the truth table in addition to the judgement that the argument in this case is valid. Finally, the user can employ the delete button '⌫' to delete the last input, the clear button 'C' to clear the whole screen, the memory store button 'MS' to put a copy of the input into memory, the memory recall button 'MR' to retrieve any stored input from memory and the memory clear button 'MC' to empty the memory store.
(D) UNDERSTANDING ERRORS:
If the input is not well-formed, the calculator indicates that this is so and, where possible, provides red underlining to pin-point the location of the error(s). In most cases, specific descriptions of the nature of non-well-formedness are also given. To be precise, the following specific errors are displayed: 'missing brackets', 'missing conclusion', 'missing connectives', 'missing parentheses', 'missing variables', 'needless parentheses', 'no { } after ╞', 'no ╞ within { }', 'no comma after ╞', 'no content outside { }', 'unequal parentheses' and 'scope ambiguity'. If, for example, the input is '(P)', then the output will be: 'not well-formed: needless parentheses'. Whenever a plus sign '+' precedes such descriptions, this means that more than one type of error has been found. To keep the output neat and simple, only one type of error is explicitly stated through a description. For example, input '((P&&Q))' contains two errors, namely 'needless parentheses' and 'missing variables', but only one is shown: 'not well-formed: + needless parentheses'.
Here is an explanation of the types of specific errors in detail:
The 'missing brackets' error indicates that one or both of the curly brackets '{ }' that denote the beginning and end of a set is/are missing. That usually happens because the user inserted a comma in the input to identify different sentences, e.g. 'P,Q', but forgot to enclose this input within a pair of brackets, i.e. '{P, Q}'. If there is a solitary sentence on the left side of a double turnstile '╞', the brackets can be dropped. That is, either 'P╞P' or '{P}╞P' is well-formed, but 'P, Q╞P' is not.
The 'missing conclusion' error comes up when the user inserts a double turnstile '╞' in the input without a sentence following it. Such a sentence is what we call a 'conclusion' in an argument. For example, the input '{P, Q}╞' is missing a conclusion. To correct this error, just insert a sentence after the previously mentioned input. For example, '{P, Q}╞P'.
The 'missing connectives' error is indicated when the input contains consecutive letter variables, e.g. 'PP', but no binary connective, i.e. '&', '∨', '→', '↔', to bind them together. To correct the error, place a binary connective between the letter variables, e.g. 'P→P'.
The 'missing parentheses' error points out that the absence of one or more pairs of parentheses, e.g. 'P&Q&R'. Any instance of a binary connective (i.e. '&', '∨', '→', '↔') together with the letter variables it binds must be enclosed within parentheses. The sole exception to this rule concerns cases where the outermost parentheses may be dropped if the user so wishes to. Thus, to correct the earlier input we can just add one or more pairs of parentheses. For example, either '(P&Q)&R' or '((P&Q)&R)'. Note also that the parentheses could have been placed around different variables. For example, either 'P&(Q&R)' or '(P&(Q&R))'.
The 'missing variables' error signifies that the input doesn't have enough letter variables. Here's one example: 'P↔∨Q'. To correct it, the user can put whatever letter variable they desire in between any two neighbouring binary connectives, making sure to also add the appropriate parentheses in the process, e.g. 'P↔(R∨Q)'. Another way to correct this error is to remove one of the logical connectives, e.g. 'P↔Q'.
The 'needless parentheses' error appears when the user has given too many pairs of parentheses to the input. For example: '((P&Q))'. This input can be corrected by removing one or both pairs of parentheses. That is, either '(P&Q)' or 'P&Q' is correct. The second of these illustrates the exception mentioned above, namely that the outermost pair of parentheses of a sentence may be dropped. Note also that input that consists solely of a single letter variable should never be enclosed in parentheses. That is, '(P)' is not well-formed but 'P' is well-formed.
The 'no { } after ╞' error signifies that the user has inserted one or more curly brackets '{ }' after the double turnstile '╞', e.g. 'P&Q╞{P,Q}'. Since, in this app, we only consider whether a set of one or more premises entails only one conclusion at a time, such input is prohibited. To correct it, remove the curly brackets plus any commas and insert just one sentence after the double turnstile, e.g. 'P&Q╞P'.
The 'no ╞ within { }' error is reported whenever the user places a double turnstile '╞' within curly brackets '{ }'. For example, '{Q╞Q∨P}'. The double turnstile must appear only after such brackets. To correct this error shift all input beginning with '╞' immediately to the right of bracket '}'. In the example just given this results in: '{Q}╞Q∨P'.
The 'no comma after ╞' error shows up when a comma is employed after the double turnstile '╞'. For example, '{P, P→Q}╞P,Q'. As explained above, this app evaluates only one conclusion at a time. To correct this error, remove any commas appearing after the double turnstile. For example, '{P, P→Q}╞Q'.
The 'no content outside { }' error is expressed whenever letter variables or connectives appear either to the left of the curly brackets, e.g. 'P&{Q}' or to the right of curly brackets but not after the double turnstile '╞', e.g.'{Q}&P' or '{Q}&P╞Q'. To correct this error, remove such content or place it within the curly brackets, e.g. '{Q}' or '{Q&P}', '{Q}╞Q' or '{Q&P}╞Q'.
The 'unequal parentheses' error is produced whenever the input contains parentheses that do not form pairs. For example, 'R∨S)' or '((P∨Q)&R'. To correct this error ensure that parentheses come in pairs. In the examples just given: '(R∨S)' and '((P∨Q)&R)'.
Finally, the 'scope ambiguity' error is generated whenever the input contains binary connectives whose range conflicts. For example, the conditional connectives '→' in '(P→(P∨Q)→Q)' are conflicting. Two binary connectives in a sentence cannot share the same content as one of the two sentences each connects. In the example just given, (P∨Q) is both the consequent for P→(P∨Q) and the antecedent for (P∨Q)→Q. To resolve this problem, the user can use parentheses to force a unique interpretation, e.g. either P→((P∨Q)→Q) or (P→(P∨Q))→Q. Note that these two sentences have different truth-tables. Though this is not always the case, it is worth bearing in mind.


